数字图像 小计

问题1：

代码

from PIL import Image

# 创建空白图像
image = Image.new("RGB", (128, 128))
# 设置颜色值
red = (255, 0, 0)
blue = (0, 0, 255)
green = (0, 255, 0)
black = (0, 0, 0)
# 填充颜色
for y in range(64):
    for x in range(64):
        image.putpixel((x, y), red)  # 左上角为红色
        image.putpixel((x, y + 64), blue)  # 左下角为蓝色
        image.putpixel((x + 64, y), green)  # 右上角为绿色
        image.putpixel((x + 64, y + 64), black)  # 右下角为黑色
# 显示图像
image.show()

问题1运行结果：

问题2

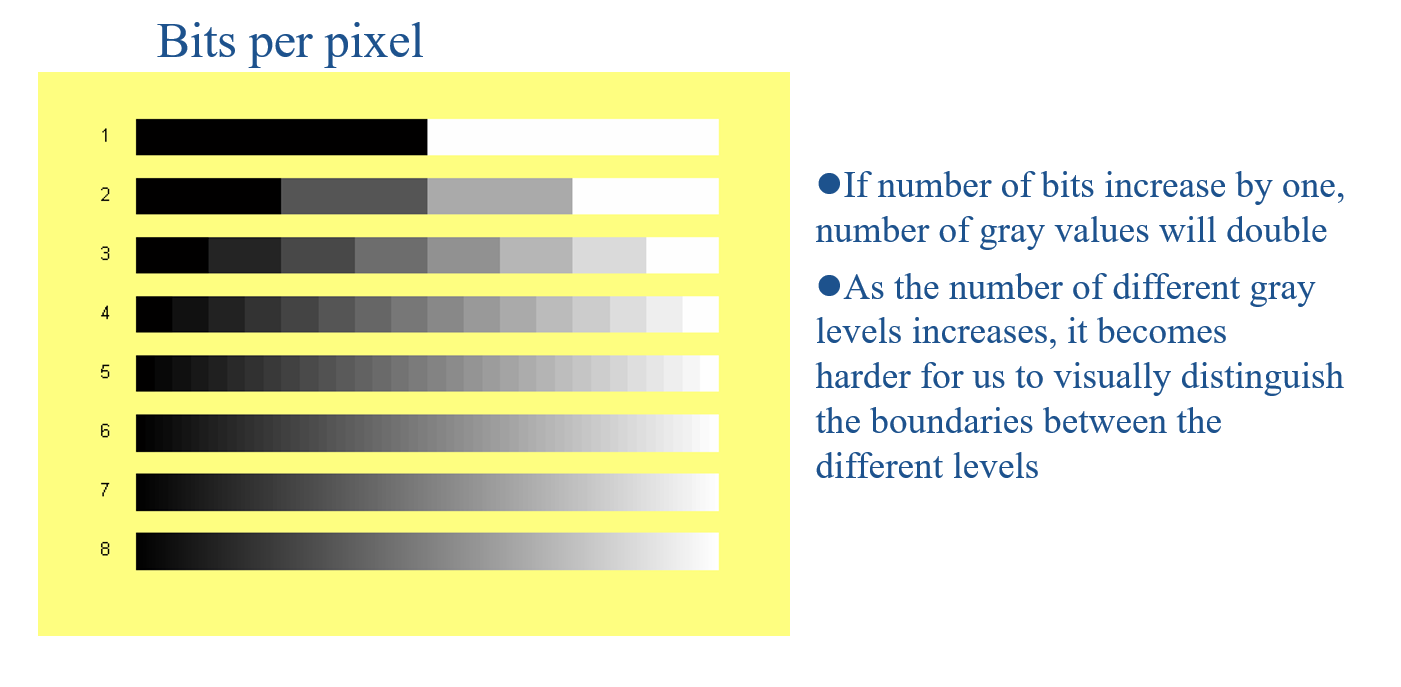
如果比特数增加了，灰度值的数量将会翻倍。随着不同灰度级别数量的增加，我们将更难以在不同级别之间视觉上区分边界。

问题解决思路：

这个问题涉及到计算灰度级数量、计算灰度级差异以及判断在不同位数下是否难以视觉区分不同灰度级。解决思路如下：

首先，根据给定的位数，计算灰度级数量。灰度级数量等于2的位数次方。
然后，根据不同的位数，计算灰度级数量之间的差异。灰度级差异等于两个位数下的灰度级数量之差。
最后，判断不同位数下是否难以视觉区分不同灰度级。若灰度级数量大于2，则认为难以区分，反之则容易区分。

代码

def calculate_gray_values(bits):
    """计算灰度级数量"""
    gray_values = 2 ** bits  # 灰度级数量等于2的bits次方
    return gray_values

def calculate_difference(bits1, bits2):
    """计算灰度级差异"""
    gray_values1 = calculate_gray_values(bits1)
    gray_values2 = calculate_gray_values(bits2)

    difference = gray_values2 - gray_values1  # 灰度级差异等于两个位数下的灰度级数量之差
    return difference

def distinguish_boundaries(bits):
    """判断在不同位数下是否难以视觉区分不同灰度级"""
    gray_values = calculate_gray_values(bits)

    if gray_values > 2:
        print("对于我们来说，视觉上区分不同级别之间的边界变得更加困难。")
    else:
        print("我们仍然能够轻松地在不同级别之间视觉上区分边界。")

# 测试代码
bits1 = 4
bits2 = bits1 + 1
gray_values1 = calculate_gray_values(bits1)
gray_values2 = calculate_gray_values(bits2)

# 输出结果
print(f"如果比特数增加一位，灰度值数量将翻倍: {gray_values2 == gray_values1 * 2}")
print(f" {bits1} 位 和 {bits2} 位 之间的灰度值差异为: {calculate_difference(bits1, bits2)}")

# 判断不同位数下是否难以视觉区分不同灰度级
distinguish_boundaries(bits1)
distinguish_boundaries(bits2)

四、这段代码的思路步骤可以总结如下：

定义一个函数calculate_gray_values(bits)，计算灰度级数量。根据输入的位数（bits），通过2的bits次方计算出灰度级数量，并返回结果。
定义一个函数calculate_difference(bits1, bits2)，计算灰度级差异。调用calculate_gray_values函数分别计算出bits1和bits2下的灰度级数量，然后用灰度级数量2减去bits1下的灰度级数量，得到灰度级差异，并返回结果。
定义一个函数distinguish_boundaries(bits)，判断在不同位数下是否难以视觉区分不同灰度级。调用calculate_gray_values函数计算出给定位数下的灰度级数量，然后根据灰度级数量是否大于2判断结果，并输出对应的提示信息。
测试代码部分，分别定义bits1和bits2的值。然后调用calculate_gray_values计算出bits1和bits2下的灰度级数量。
输出结果，打印比特数增加一位后灰度值数量翻倍的结果，并打印bits1位和bits2位之间的灰度值差异。
调用distinguish_boundaries函数，判断不同位数下是否难以视觉区分不同灰度级，并输出结果。先传入bits1进行判断，再传入bits2进行判断。

题目2代码运行结果

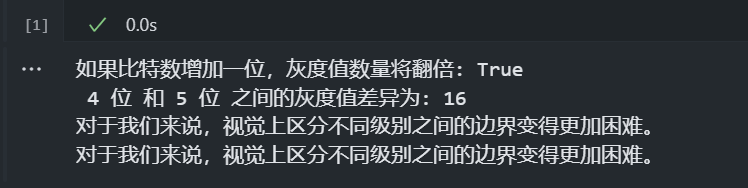
结论

这段代码实现了灰度级数量的计算、灰度级差异的计算以及不同位数下是否难以视觉区分的判断。
运行代码后，会输出计算结果和判断结果。根据示例运行结果，我们可以得出结论：增加一位的位数，灰度级数量会翻倍；
不同位数下的灰度级差异为16；当位数增加时，难以视觉区分不同灰度级。

问题3：

代码：

from PIL import Image
from matplotlib import pyplot as plt
import numpy as np

# 打开原始图像
image = Image.open("xxx.jpg")
# 将图像转换为灰度图像
gray_image = image.convert("L")
# 进行4倍减采样
image_4x = gray_image.resize((image.width // 4, image.height // 4))
# 进行16倍减采样
image_16x = gray_image.resize((image.width // 16, image.height // 16))
# 将图像转换为NumPy数组
np_image1 = np.array(image_4x)
np_image2 = np.array(image_16x)
# 创建一个包含两个子图的画布
fig, (ax1, ax2) = plt.subplots(1, 2)
# 在第一个子图中显示第一个图像
ax1.imshow(np_image1, cmap='gray')
ax1.set_title('Image 1 4x downsampling')
# 在第二个子图中显示第二个图像
ax2.imshow(np_image2, cmap='gray')
ax2.set_title('Image 16x downsampling')
# 隐藏坐标轴
ax1.axis('off')
ax2.axis('off')
# 调整子图之间的间距
plt.subplots_adjust(wspace=0.2)
# 显示图像
plt.show()

问题3运行结果：

问题4：

代码：

from PIL import Image

def convert_to_grayscale(image, levels):
    # 转换为灰度图像
    grayscale_image = image.convert('L')
    
    # 调整灰度级别
    grayscale_images = []
    for level in levels:
        factor = 256 // level
        converted_image = grayscale_image.point(lambda x: x // factor * factor)
        grayscale_images.append(converted_image)
    
    return grayscale_images

from PIL import Image

def display_images(images):
    # 创建一个新的图片，用于显示多个灰度图像
    width, height = images[0].size
    result_image = Image.new('L', (width * 3, height * 2))

    # 将灰度图像按顺序拼接到一张图片上
    for i, image in enumerate(images[:3]):
        result_image.paste(image, (i * width, 0))

    for i, image in enumerate(images[3:]):
        result_image.paste(image, (i * width, height))

    # 显示图片
    result_image.show()

# 打开原始图片
original_image = Image.open('xxx.jpg')
# 定义要转换的灰度级别
levels = [256, 64, 16, 8, 4, 2]
# 将图片转换为不同的灰度级图像
grayscale_images = convert_to_grayscale(original_image, levels)
# 在一张图片内显示灰度级图像
display_images(grayscale_images)

数字图像小计